
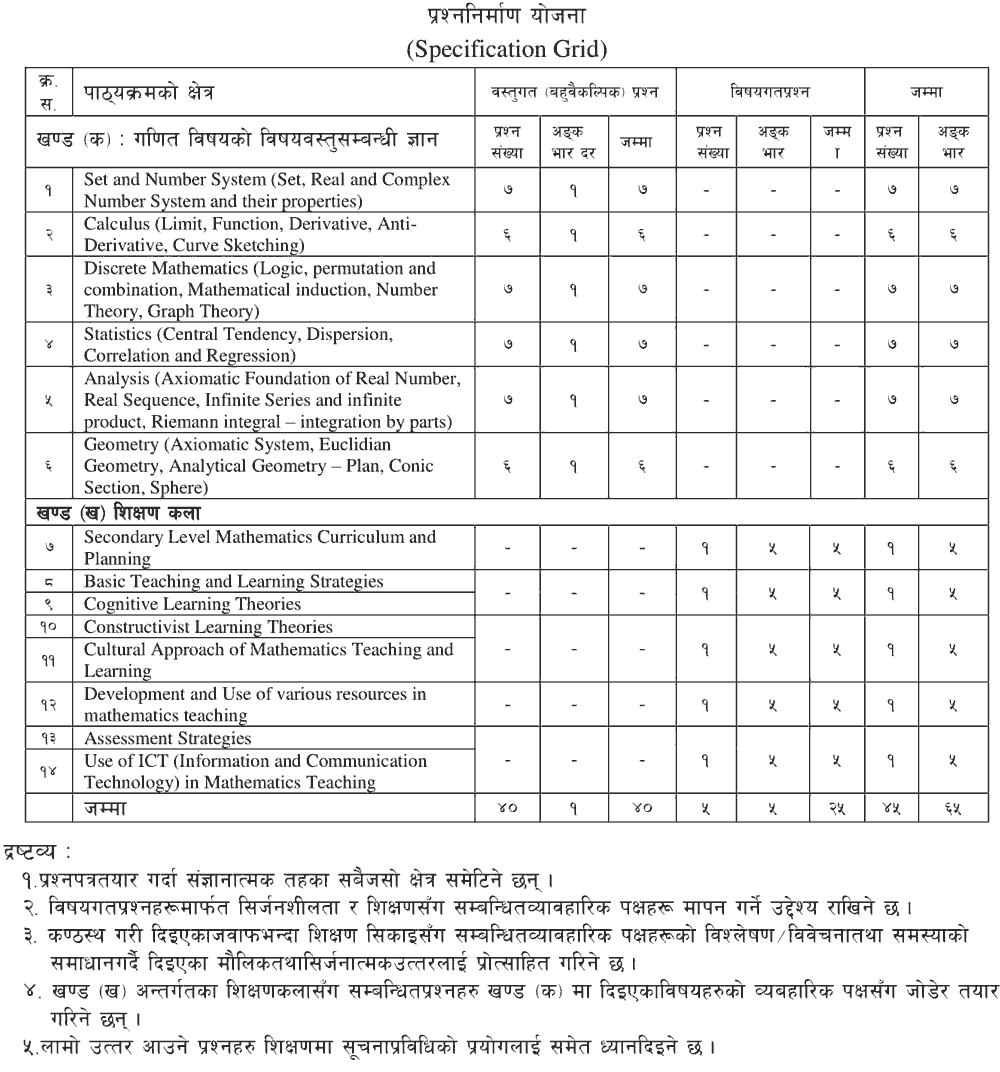
- Set and Number System: Set, Real, and Complex Number System and their properties.
1.1 Set and Notations, the relation between sets, operations on set, algebra of sets, denumerable sets and its cardinality, open and closed set/intervals
1.2 Real Number system: Properties of a real number, order axiom, the absolute value of a real number, Boundedness property, supremum and infimum of a subset of real numbers, completeness axiom.
1.3 Complex number system: Imaginary unit, complex numbers and its geometrical interpretation, a conjugate of a complex number, the absolute value of a complex number, square root of a complex number, polar form of a complex number.
- Calculus: Function, Limit, continuity, Derivative, Anti-Derivative, Curve Sketching.
2.1 Concept of function, Meaning of x- a limit of an algebraic function, infinity as a limit of a function, limit of a trigonometric function, limit of the logarithmic and exponential and absolute value function
2.2 Left hand and right-hand limit, Concept of continuities and discontinuities of a function, type of discontinuity (ordinary, removable and infinite)
2.3 Relationship between continuity and differentiability of a function, Definition of tangent as the limit of secant line, derivative of function and its geometrical meaning, basic techniques of differentiation (sum rule, product rule, power rule, quotient rule, chain rule), differentiating algebraic, trigonometric, logarithm and exponential function, increasing and decreasing function, maximum and minimum value of a function in an interval.
2.4 Concept of antiderivatives, Technique of integration, integration of basic algebraic and trigonometric function, area as a definite integral
2.5 Even function, odd function, symmetricity of the function, increasing and decreasing function, periodicity of the function, Characteristics (and curve sketching) of linear, parabolic, hyperbolic, circular, asymptotic, cubic, trigonometric and logarithmic function)
- Discrete Mathematics (Logic, permutation and combination, Mathematical induction, Number Theory, Graph Theory)
3.1 Statements, logical connectives, conditional and bi-conditional statements, truth table, tautology and contradiction, arguments, Euler diagram
3.2 Basic principle of counting, the arrangement of objects in different cases (all different, not all different, circular), selection of objects (combination) and its properties
3.3 Concept of mathematical induction, mathematical induction as a method of proof, its general process
3.4 Fundamental concepts in number theory (well-ordering principle, order axiom, trichotomy law, prime, and composite. etc.), Divisibility theory and its properties, GCD and its properties, relatively prime numbers, fundamental theorem of arithmetic, the concept of linear Diophantine equation, congruence modulo and its properties, the divisibility test,
3.5 Basic concepts (vertex, edge, graph, degree of a vertex, parallel edges, loop, simple graph, empty and null graph, adjacent vertices, pendant vertex and edge, isolated vertex, multi-graph), the relation between vertex and edge in a graph, complete graph, concept of walk, path, trail, cycle, dis/connected graph, concept of subgraph, the Konigsberg Bridge problem,
3.6 Eulerial circuit and Eulerian trail, Hamiltonian circuit
3.7 Concept of tress and basic properties, the concept of dia-graph
- Statistics (Central Tendency, Dispersion, Correlation and Regression, Skewness)
4.1 Concept and appropriate use of the measure of central tendencies (mean, median, mode) and quartile values.
4.2 Concept and appropriate use of the measure of dispersion (range, QD, MD, SD) and coefficient of variation
4.3 Correlation and regression analysis
4.4 Use of skewness
- Analysis (Axiomatic Foundation of Real Number, Real Sequence, Infinite Series and infinite product, Riemann integral - integration by parts)
5.1 Axiomatic Foundation of Real Number
5.2 Sequence, boundedness of sequences, upper and lower limit points of bounded sequences, Non/convergent
sequences, monotonic sequences
5.3 Meaning of infinite series, convergent series, a different test of convergence series, series of positive and negative terms, a product of infinite series
- Geometry (Axiomatic System, Euclidian Geometry, Analytical Geometry - Plan, Conic Section, Sphere)
6.1 Axiomatic system and their properties (Fe's and Fo's)
6.2 Euclidian geometry
6.3 Analytical geometry
6.3.1 Conic section: parabola, ellipse, hyperbola;
6.3.2 Plane: general equation, various form of the equation of a plane, the angle between two planes, the angle between line and plane, the plane through the intersection of two planes, length of the perpendicular from a point to a plane, the bisector of angle
6.3.3 Sphere: general equation of a sphere, equation of sphere with the given diameter, equation of tangent plane on a sphere
Part: Two
Teaching Learning Process/Pedagogical Knowledge Full Marks: 25
- Secondary Level Mathematics Curriculum and Planning: Yearly-Lesson, unit and daily lesson plan, curriculum development models, curriculum design
- Basic Teaching and Learning Strategies: Collaborative and Cooperative, Inductive and Deductive, Analytic and Synthesis, Conceptual and Procedural, Laboratory, Project, Problem Solving, Heuristic
- Cognitive Learning Theories: Piaget's, Bruner's and Vygotsky's learning theories
- Constructivist Learning Theories: Trivial/personal, Social and Radical learning theories
- Cultural Approach of Mathematics Teaching and Learning: culturally contextualized mathematics teaching, culturally responsive pedagogy and ethnomathematics/ ethno-pedagogy
- Development and Use of various resources in mathematics teaching
- Assessment Strategies (Written/Project Work/Presentation/Field Work): Measurement and Evaluation, Formative and Summative Evaluation, CAS, types of test, Standardization of test
- Use of ICT (Information and Communication Technology) in Mathematics Teaching
14.1 ICT for Continuous Professional Development: Information retrieve/search/manage, knowledge on ICT competencies
14.2 ICT for content enhancement: Use of various ICT tools to explore mathematical knowledge
14.3 ICT as a delivery tool: Use of ICT - Mobile, Multi-media, software, online materials, etc. in classroom teaching for specific mathematical contents

Group B (Subjective Questions) (5 x 5 = 25)
- What is the vertical and horizontal organization of the curriculum? Do you feel the curriculum of compulsory mathematics of grade ten is vertically and horizontally well organized? Give your arguments with appropriate pieces of evidence.
- How the processes of learning mathematics among children are different from an adult? And, write your understanding about `how children learn?' with reference to the assumptions of behaviorism, cognitivism, and constructivism.
- Assume that you are introducing "Limit" to your students for the first time. What activities do you perform in the class of 45 minutes? Discuss.
- How do you use local resources in teaching school mathematics? Choose any one of the mathematical concepts from grades 9-12 (based on school curriculum) and discuss the use of local resources to teach that concept.
- CAS (Continuous Assessment System) is assumed as one of the best tools/approaches for assessing the overall performance of the students. Do you agree with this statement? Justify your arguments.
Please Download Collegenp App from Playstore: Install Now for regular Update


